Python函数进阶
一、作业回顾
1、格式化输出与%百分号
以下结果中,可以正常输出“50%及格”语句是(B)
A、print("%d%及格" % (50)) => 回答大部分结果(Python这种写法不正确)
B、print("%d%%及格" % (50)) => 正确结果
2、字符串切片
定义一个字符串str1 = 'abcdefg',使用切片截取字符串str1[3::-2],求返回结果:(C)
C、'db'
3、字典的定义
其实字典中的key可以是很多数据类型(不可变数据类型 => 整型、浮点型、字符串、元组)
my_dict = {}
my_dict[1] = 1
my_dict['1'] = 2
my_dict[1.0] = 3
print(my_dict[1] + my_dict['1'] + my_dict[1.0])二、引用变量与可变、非可变类型
1、引用变量
在大多数编程语言中,值的传递通常可以分为两种形式“值传递与引用传递”,但是在Python中变量的传递基本上都是引用传递。
☆ 聊聊变量在内存底层的存储形式
a = 10第一步:首先在计算机内存中创建一个数值10(占用一块内存空间)
第二步:在栈空间中声明一个变量,如a
第三步:把数值10的内存地址赋予给变量小a,形成所谓的**“引用关系”**

☆ 如何验证Python中变量的引用关系
答:可以使用内置方法id(),其参数就是要显示的变量信息 => id(变量名称)
a = 10
print(id(a))☆ 把一个变量赋予给另外一个变量的影响
a = 10
b = a
print(id(a))
print(id(b))运行结果:

说明:由以上运行结果可知,当我们把一个变量赋予给另外一个变量时,其两者指向的内存地址相同。就说明a和b指向了同一块内存空间,原理图如下:
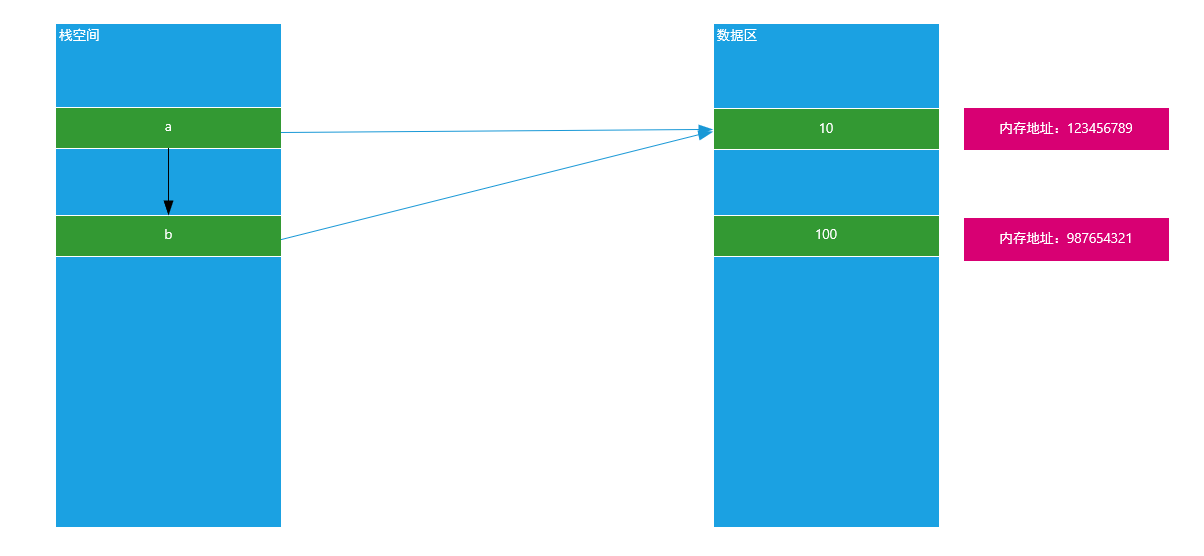
思考:如果在b = a以后,我们改变了变量a的值,问变量b是否会受到影响?
#a = 10
#print(id(a))
a = 10
b = a
a = 100
print(b) # 10 或 100
print(id(a))
print(id(b))原理图:
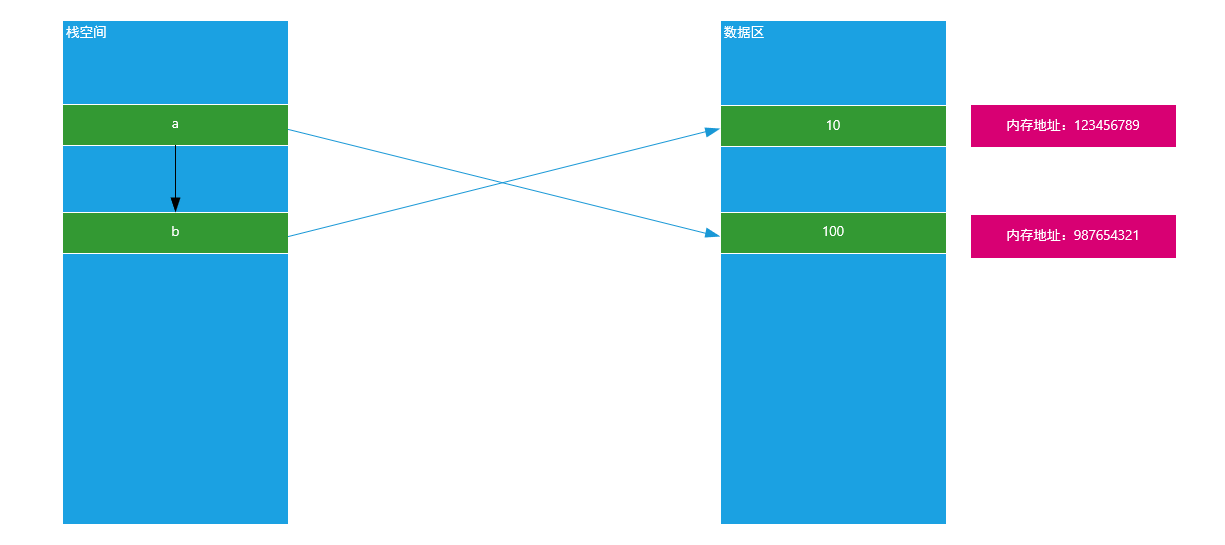
总结:不可变数据类型(数值)在赋值以后,其中一个值的改变不影响另外一个变量,因为两者指向空间地址不同。
2、Python中可变和非可变数据类型
☆ 问题1:在Python中一共有几种数据类型?
答:7种,数值(int整型、float浮点类型)、bool类型(True和False)、字符串类型(str)、元组(tuple 1,2,3)、列表(list [1, 2, 3])、字典(dict {key:value})、集合(set {1, 2})
在Python中,我们可以把7种数据类型分为两大类:可变类型 + 非可变类型
① 非可变类型
数值(int整型、float浮点类型)
bool类型(True和False)
字符串类型(str)
元组(tuple 1,2,3)
② 可变类型
列表(list [1, 2, 3])
字典(dict {key:value})
集合(set {1, 2})
☆ 问题2:如何判断一个数据类型是可变类型还是非可变类型?
在Python中,可变类型与非可变类型主要是通过这个数据类型在内存中的表现形式来进行定义的。
① 可变类型就是在内存中,其内存地址一旦固定,其值是可以发生改变的
a = [1, 2, 3]
print(id(a))
#向内存中追加新数据(对数据进行改变只能通过数据类型.方法()实现)
a.append(4)
print(id(a))原理图:
② 非可变类型就是在内存中,内存地址一旦固定,其值就没办法发生任何改变了
a = 10
print(id(a))
a = 'hello'
print(id(a))原理图:
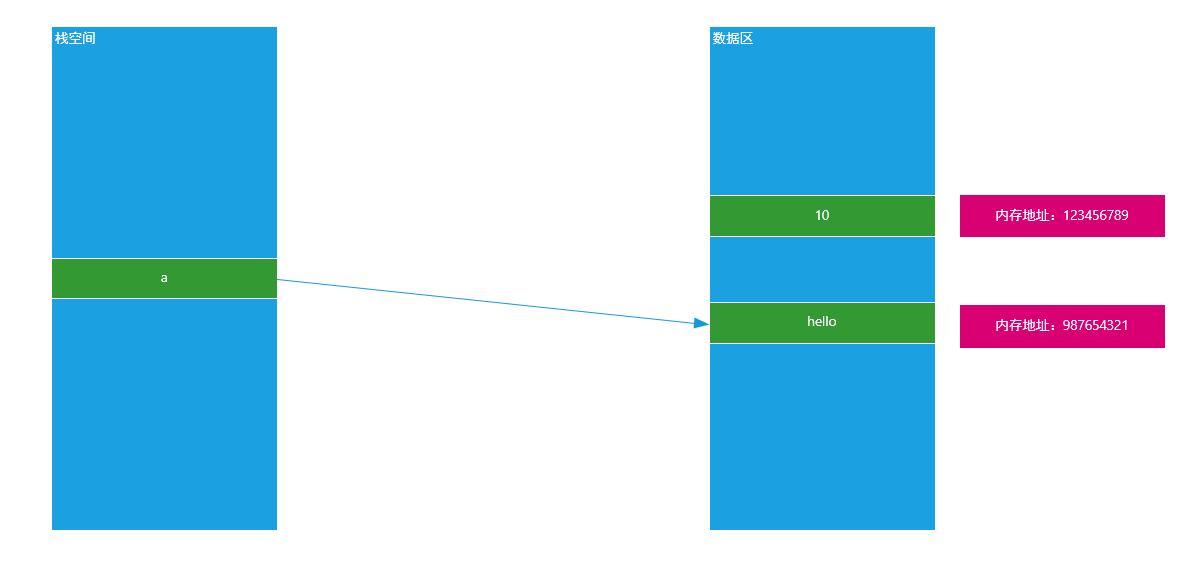
3、可变类型与非可变类型在函数中的应用
☆ 可变类型
#定义一个函数
def func(names):
print(names)
#定义一个全局变量
names = ['张三', '李四', '王五']
#调用函数
func(names)原理图:
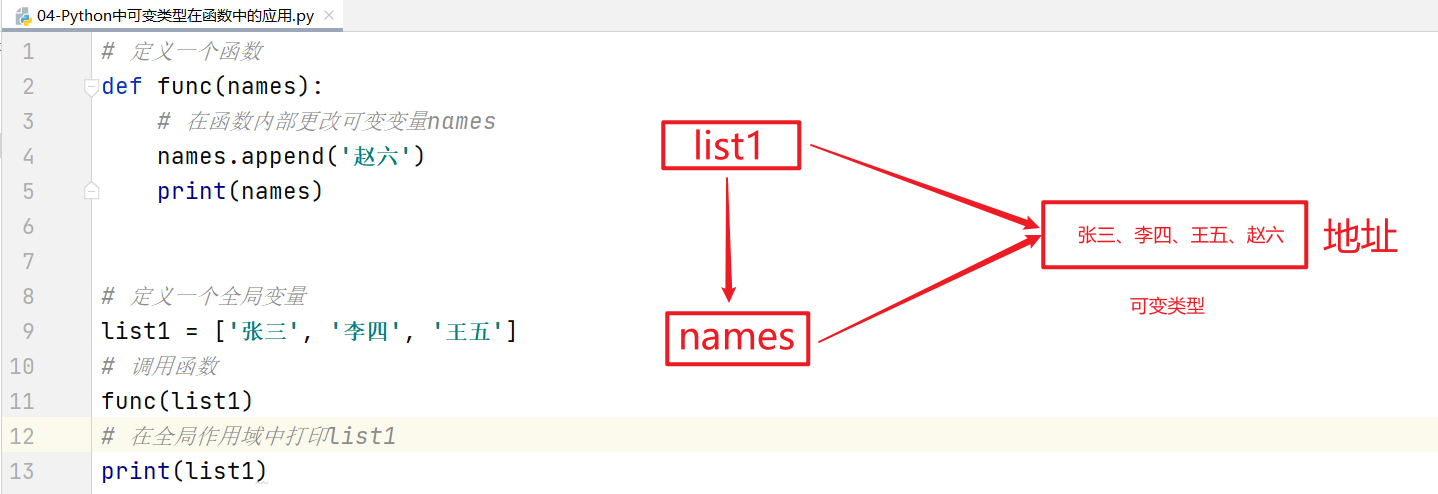
综上所述:可变类型在函数中,如果在全局或局部中对可变类型进行增删改操作,其外部和内部都会受到影响。
☆ 不可变类型
#定义一个函数
def func(num):
num += 1
print(num)
#定义一个全局变量
a = 10
#调用函数
func(a)
#在全局作用域中打印a
print(a)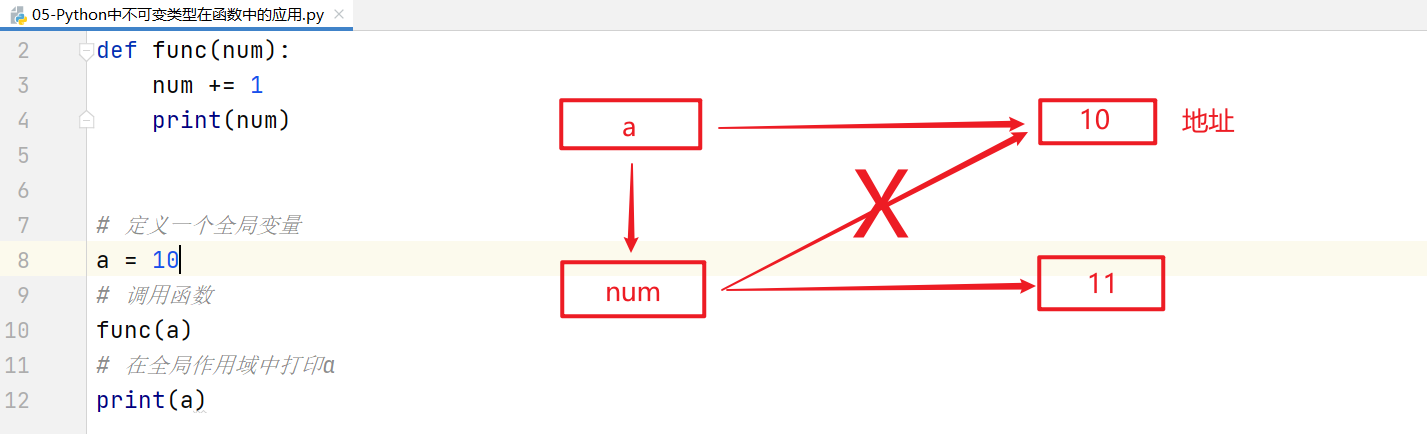
综上所述:不可变类型在函数中,局部或全局的改变对外部和内部都没有任何影响。
三、函数递归(重点难点)
1、前言
编程思想:如何利用数学模型,来解决对应的需求问题;然后利用代码实现对应的数据模
算法:使用代码实现对应的数学模型,从而解决对应的业务问题
程序 = 算法 + 数据结构
在我们经常使用的算法中,有两种非常常用的算法:递推算法 + 递归算法,专门用于解决一些比较复杂,但是拆分后相似度又非常高的程序。
2、递推算法
递归算法:递推算法是一种简单的算法,即通过已知条件,利用特定条件得出中间推论,直至得到结果的算法。递推又分为顺推和逆推。
顺推:通过最简单的条件,然后逐步推演结果
逆推:通过结果找到规律,然后推导已知条件
递推算法案例:斐波那契数列
1 1 2 3 5 8 13 21 ...
① ② ③ ④ ⑤ ⑥ ...
第1位为1,第2位为1,第3位为2 = 1 + 1,第4位为3 = 2 + 1,依次类推...第n位结果为多少?
f(n) = f(n-1) + f(n-2)
提出问题:求斐波那契数列第15位的结果?
分析:f(15) = f(14) + f(13)
f(14) = f(13) + f(12)
f(13) = f(12) + f(11)
...
f(4) = f(3) + f(2) = 3 + 1
f(3) = f(2) + f(1) = 2
f(2) = 1
f(1) = 1
递推算法:使用while循环或for循环
#递推算法:根据已知条件,求结果(或者根据结果求未知条件)
def recusive(n):
""" 返回斐波那契数列某一位(n>=1)的结果 """
if n == 1 or n == 2:
return 1
# 开始递推f(3) = f(2) + f(1) f(4) = f(3) + f(2) ... f(15) = f(14) + f(13)
dict1 = {1:1, 2:1}
for i in range(3, n+1):
# f(3) = f(2) + f(1)
# f(i) = f(i-1) + f(i-2)
dict1[i] = dict1[i-1] + dict1[i-2]
return dict1[n]
#函数调用
print(recusive(15))3、什么是递归算法
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
① 简化问题:找到最优子问题(不能再小) ② 函数自己调用自己
def func():
# 自己调用自己
func()
func()4、递归两种重要的元素
递归有两个非常重要的概念:
① 递归点:找到解决当前问题的等价函数(先解决规模比当前问题小一些的函数,依次类推,最终实现对问题的解决) => 有递有归
② 递归出口:当问题解决的时候,已经到达(必须存在)最优问题,不能再次调用函数了
注:如果一个递归函数没有递归出口就变成了死循环
5、编写递归三步走
① 明确你这个函数想要干什么
如:求斐波那契数列
② 寻找递归结束条件
如:就是在什么情况下,递归会停止循环,返回结果
③ 找出函数的等价关系式
如:斐波那契数列,第n位 f(n) = f(n-1) + f(n-2)
案例1:使用递归求斐波那契数列
第一步:明确这个函数想要干什么(先定义出来,明确调用方式)
#斐波那契数列 1 1 2 3 5 8 13 21 ...
def f(n):
# 编写递归代码求第n位的结果
#调用函数
print(f(15)) # 610第二步:寻找递归的结束条件
#斐波那契数列 1 1 2 3 5 8 13 21 ...
def f(n):
# 编写递归代码求第n位的结果
if n == 1 or n == 2:
return 1
#调用函数
print(f(15)) # 610第三步:找出函数的等价关系式(最关键的一步)
#斐波那契数列 1 1 2 3 5 8 13 21 ...
def f(n):
# 编写递归代码求第n位的结果
if n == 1 or n == 2:
return 1
# 找出与斐波那契数列等价的关系式
return f(n-1) + f(n-2)
#调用函数
print(f(15)) # 610案例2:使用递归求N的阶乘(如n=100)
阶乘是什么?一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,如:n!=1×2×3×...×(n-1)×n
1! = 1
2! = 1x2 = 2
3! = 1x2x3 = 6
4! = 1x2x3x4 = 24
...
n!=1×2×3×...×(n-1)×n
第一步:明确这个函数要做什么以及定义函数以及调用方式
def f(n):
# 编写递归条件
print(f(100))第二步:寻找递归的结束条件
def f(n):
# 编写递归结束条件
if n <= 2:
return n
# ...递归等式
print(f(100))第三步:编写递归等价公式(自己要调用自己)
等价公式 = 找规律
1! = f(1) = 1
2! = f(2) = 2
3! = f(2)x3 = 6
4! = f(3)x4 = 24
...
n!= f(n-1) * n
def f(n):
# 编写递归结束条件
if n <= 2:
return n
# ...递归等式
return f(n-1) * n
print(f(100))案例3:面试题 => 猴子吃桃问题
猴子吃桃问题。猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半另加一个。到第10天早上想再吃时,就只剩下一个桃子了。求第1天共摘了多少个桃子
第一步:确定函数主要要完成什么功能,需要传递哪些参数,确认调用方式
def f(n):
# 编写递归代码
#调用f函数
print(f(1))第二步:编写递归的结束条件(出口)
#第一步:确定函数功能
def f(n):
# 第二步:编写递归结束条件(出口)
if n == 10:
return 1
#调用函数
print(f(1))第三步:找出与这个问题相等的等式关系
求桃子的剩余数量?假设法:假设有10个桃子
第1天,10个桃子吃一半,10/2 = 5 + 1 = 6
第2天,4个桃子吃一半,4/2 = 2 + 1 = 3
第3天,再想吃剩1个
第n天,总剩余桃子的数量 = (第(n+1)天桃子的剩余桃子的数量 + 1) * 2
#第一步:确定函数功能
def f(n):
# 第二步:编写递归结束条件(出口)
if n == 10:
return 1
# 第三步:寻找与这个问题相似的等价公式
return (f(n+1) + 1) * 2
#调用函数
print(f(8))四、lambda表达式
1、普通函数与匿名函数
在Python中,函数是一个被命名的、独立的完成特定功能的一段代码,并可能给调用它的程序一个返回值。
所以在Python中,函数大多数是有名函数 => 普通函数。但是有些情况下,我们为了简化程序代码,也可以定义匿名函数 => lambda表达式
2、lambda表达式应用场景
如果一个函数有一个返回值,并且只有一句代码,可以使用 lambda简化。
3、lambda表达式基本语法
变量 = lambda 函数参数:表达式(函数代码 + return返回值)
#调用变量
变量()4、编写lambda表达式
定义一个函数,经过一系列操作,最终返回100
def fn1():
return 100
#调用fn1函数
print(fn1) # 返回fn1函数在内存中的地址
print(fn1()) # 代表找到fn1函数的地址并立即执行lambda表达式进行简化:
fn2 = lambda : 100
print(fn2) # 返回fn2在内存中的地址
print(fn2())5、编写带参数的lambda表达式
编写一个函数求两个数的和
def fn1(num1, num2):
return num1 + num2
print(fn1(10, 20))lambda表达式进行简化:
fn2 = lambda num1, num2:num1 + num2
print(fn2(10, 20))6、lambda表达式相关应用
☆ 带默认参数的lambda表达式
fn = lambda a, b, c=100 : a + b + c
print(fn(10, 20))☆ 不定长参数:可变参数*args
fn1 = lambda *args : args
print(fn1(10, 20, 30))☆ 不定长参数:可变参数**kwargs
fn2 = lambda **kwargs : kwargs
print(fn2(name='Tom', age=20, address='北京市海淀区'))☆ 带if判断的lambda表达式
fn = lambda a, b : a if a > b else b
print(fn(10, 20))☆ 列表数据+字典数据排序(重点)
知识点:列表.sort(key=排序的key索引, reverse=True)
students = [
{'name': 'Tom', 'age': 20},
{'name': 'Rose', 'age': 19},
{'name': 'Jack', 'age': 22}
]
#按name值升序排列
students.sort(key=lambda x: x['name'])
print(students)
#按name值降序排列
students.sort(key=lambda x: x['name'], reverse=True)
print(students)
#按age值升序排列
students.sort(key=lambda x: x['age'])
print(students)执行流程:
students = [
{'name': 'Tom', 'age': 20},
{'name': 'Rose', 'age': 19},
{'name': 'Jack', 'age': 22}
]
#按name值升序排列
students.sort(key=lambda x:x['name'])
print(students)五、Python中高阶函数
1、什么是高阶函数
把函数作为参数传入,这样的函数称为高阶函数,高阶函数是函数式编程的体现。函数式编程就是指这种高度抽象的编程范式。
2、高阶函数的由来
abs()返回绝对值。
abs(-10) # 10round()函数可以完成对数字的四舍五入计算。
round(1.2) # 1
round(1.9) # 2sum() 求和。
sum([1,2,3]) # 6需求:任意两个数字,按照指定要求(① 绝对值 ② 四舍五入)整理数字后再进行求和计算。
def fn1(num1, num2):
return abs(num1) + abs(num2)
print(fn1(-10, 10))def fn2(num1, num2):
return round(num1) + round(num2)
print(fn2(10.2, 6.9))要求:我们能不能对以上进行简化,然后合并为同一个函数 => 设计思想(高阶函数)
def fn(num1, num2, f):
# f代表要传入的参数(参数是一个函数名,如abs或round)
return f(num1) + f(num2)
#绝对值求和
print(fn(-10, 10, abs))
#四舍五入
print(fn(10.2, 6.9, round))3、map()函数
map(func, list),将传入的函数变量func作用到list变量的每个元素中,并将结果组成新的列表(Python2)/迭代器(Python3)返回。
#使用map对lst进行func函数操作
list2 = list(map(lambda x:x**2, list1))
print(list2) # [1, 4, 9]4、reduce()函数
reduce(func,list)用于将一个可迭代对象(如列表、元组等)通过一个二元操作函数进行累积操作,最终返回一个单一的值。其中func必须有两个参数。每次func计算的结果继续和序列的下一个元素做累加计算。
注意:reduce()传入的参数func必须接收2个参数。
from functools import reduce #reduce()不是内置函数,需导入模块
sums = reduce(lambda a,b:a+b, [1,2,3])
print(sums) # 65、filter()函数
filter(func, list)函数用于过滤序列, 过滤掉不符合条件的元素, 返回一个 filter 对象。如果要转换为列表, 可以使用 list() 来转换。
#定义一个序列
list1 = [1, 2, 3, 4, 5, 6, 7, 8]
#调用filter函数进行过滤操作
result = filter(lambda n:n%2**0, list1)
print(list(result)) # [2, 4, 6, 8]6、zip()函数
zip() 将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组。
list1 = ['a','b','c']
list2 = [1,2]
result = list(zip(list1,list2))
print(result) # [('a', 1), ('b', 2)]六、闭包
闭包(Closure)是Python中的一个重要概念,它与函数的作用域和生命周期有关。闭包允许一个函数记住并访问其在定义时所在作用域的变量,即使这个函数在其原始作用域之外被调用。
闭包的定义
闭包是一个函数对象,它具有以下两个特性:
- 该函数是在另一个函数内部定义的。
- 该函数引用了外部函数的局部变量或参数。
当外部函数返回这个内部函数时,就形成了一个闭包。闭包能够记住并访问其创建时的局部作用域中的变量。
闭包的实现
闭包的实现依赖于嵌套函数和作用域规则。在Python中,函数可以访问其定义时所在作用域的变量,这就是闭包的基础。
示例1:简单的闭包
def outer_function(x):
def inner_function(y):
return x + y
return inner_function
closure = outer_function(10)
result = closure(5)
print(result) # 输出 15在这个例子中,outer_function是外部函数,inner_function是在outer_function内部定义的闭包。inner_function引用了outer_function的局部变量x。当outer_function返回inner_function时,inner_function仍然可以访问x的值。
示例2:使用闭包实现计数器
def counter():
count = 0
def inner_function():
nonlocal count
count += 1
return count
return inner_function
counter_instance = counter()
print(counter_instance()) # 输出 1
print(counter_instance()) # 输出 2
print(counter_instance()) # 输出 3在这个例子中,counter函数返回了一个内部函数inner_function,这个内部函数通过nonlocal关键字声明了对外部函数局部变量count的访问。每次调用counter_instance时,count的值都会增加。
闭包的作用
闭包可以用来实现一些特殊的功能,例如:
- 保护外部函数的局部变量:闭包可以防止外部代码直接修改外部函数的局部变量。
- 实现数据隐藏和封装:闭包可以将一些变量隐藏在函数内部,只通过特定的接口来访问和修改这些变量。
- 实现特殊功能:闭包可以用来实现一些特殊的功能,如装饰器、记忆化等。
注意事项
- 闭包会使得外部函数的局部变量的生命周期延长,因为这些变量在外部函数执行完毕后不会被回收,而是被闭包所引用。
- 闭包的使用需要谨慎,因为不当的使用可能会导致内存泄漏等问题。
七、装饰器
装饰器是Python中一个非常强大的特性,它允许你在不修改原函数代码的情况下,为函数添加新的功能。装饰器在很多场景下都非常有用,比如日志记录、性能测试、权限校验等。
装饰器的基本概念
装饰器是一个接受函数作为参数的函数,它返回一个新的函数,这个新函数通常会在原函数执行前后添加一些额外的操作。
装饰器的使用
装饰器的使用非常简单,只需要在需要装饰的函数上方使用@装饰器名语法即可。
示例1:无参数的装饰器
def my_decorator(func):
def inner(*args, **kwargs):
print("装饰器添加的额外功能")
return func(*args, **kwargs)
return inner
#装饰器语法糖本质是 say_hello = my_decorator(say_hello)
@my_decorator
def say_hello(name):
"""简单的打招呼函数"""
print(f"你好,{name}")
say_hello("世界")输出:
装饰器添加的额外功能
你好,世界示例2:带参数的装饰器
带参数的装饰器稍微复杂一些,因为装饰器本身也是一个函数,所以需要使用嵌套函数来实现。
def decorator_with_args(arg1, arg2):
def actual_decorator(func):
def inner(*args, **kwargs):
print(f"Decorator arguments: {arg1}, {arg2}")
func(*args, **kwargs)
return inner
return actual_decorator
@decorator_with_args("arg1", "arg2")
def say_something(something):
print(something)
say_something("Hello again!")输出:
Decorator arguments: arg1, arg2
Hello again!示例3:@wraps的使用
@wraps(func)是Python装饰器中的一个常用语法,它的作用是将被装饰函数的一些属性(如函数名、文档字符串等)复制到装饰器内部的包装函数上,以保持原函数的元信息不变。这在调试和文档生成等场景中非常有用。
不使用@wraps的使用导致的问题:
def my_decorator(func):
def inner(*args,**kwargs):
return func(*args,**kwargs)
return inner
def test():
print('我是:',test.__name__)
@my_decorator
def test1():
print('我是:',test1.__name__)
test() # 我是: test
test1() # 我是: inner可以看到,被装饰后的函数名变成了inner,而不是原来的test。这是因为在装饰器内部,我们返回了一个新的函数inner,而这个函数没有保留原函数test的元信息。
为了解决这个问题,我们可以在装饰器中使用@wraps(func)来复制原函数的属性:
from functools import wraps
def my_decorator(func):
@wraps(func)
def inner(*args,**kwargs):
return func(*args,**kwargs)
return inner
def test():
print('我是:',test.__name__)
@my_decorator
def test1():
print('我是:',test1.__name__)
test() # 我是: test
test1() # 我是: test1装饰器的原理
装饰器的原理是基于闭包的。闭包是一个函数对象,它有两个特性:1. 该函数是在另一个函数内部定义的;2. 该函数引用了外部函数的局部变量或参数。当外部函数返回这个内部函数时,就形成了一个闭包。闭包能够记住并访问其创建时的局部作用域中的变量。
装饰器的应用场景
装饰器可以用来实现很多功能,以下是一些常见的应用场景:
- 日志记录:在函数执行前后记录日志,方便追踪和调试。
- 性能测试:计算函数执行的时间,用于性能分析和优化。
- 权限校验:在函数执行前检查用户权限,确保只有合适的用户可以访问特定的功能。
- 缓存:将函数的结果缓存起来,避免重复计算。
- 数据验证:在函数执行前对输入数据进行验证,确保数据的合法性。
注意事项
- 装饰器会替换掉原来的函数,所以在使用装饰器后,原函数的名字会被装饰器中的函数替代。如果需要保留原函数的名字,可以使用
functools.wraps来修饰内部函数。 - 装饰器可以叠加使用,多个装饰器会按照从上到下的顺序依次执行。
- 装饰器可以应用于类的方法,但需要稍微修改一下装饰器的实现。
